TESTE POST

Perfeito, Rafael 🚀. Vou estruturar um post didático e completo, que mistura teoria, código e visualização. Assim você pode compartilhar com colegas ou usar como material de estudo.

📘 Derivada via Limites e Aplicação em Circuitos

A derivada é um conceito fundamental em cálculo, e pode ser entendida como o limite da taxa de variação de uma função.
No contexto de circuitos elétricos, a tensão no indutor é dada por:

$$ V_L = L \cdot \frac{di}{dt} $$

Ou seja, a tensão depende da derivada da corrente em relação ao tempo.

🔎 Como calcular numericamente?

Se temos a corrente (i(t)) amostrada em um vetor, podemos aproximar a derivada usando diferenças finitas:

[ \frac{di}{dt} \approx \frac{i[k] - i[k-1]}{\Delta t} ]

Isso pode ser implementado facilmente com um laço FOR.

💻 Código em Python

import numpy as np import matplotlib.pyplot as plt # Parâmetros L = 0.5 # Indutância em Henry dt = 0.01 # Passo de tempo t = np.arange(0, 10, dt) # Corrente simulada (exemplo: seno) i = np.sin(t) # Derivada aproximada usando laço FOR di_dt = np.zeros_like(i) for k in range(1, len(i)): di_dt[k] = (i[k] - i[k-1]) / dt # Tensão no indutor V_L = L * di_dt # Gráficos plt.figure(figsize=(10,6)) plt.subplot(2,1,1) plt.plot(t, i, label='Corrente i(t)') plt.ylabel('i(t)') plt.legend() plt.subplot(2,1,2) plt.plot(t, V_L, color='red', label='Tensão V_L(t)') plt.xlabel('Tempo [s]') plt.ylabel('V_L(t)') plt.legend() plt.tight_layout() plt.show()

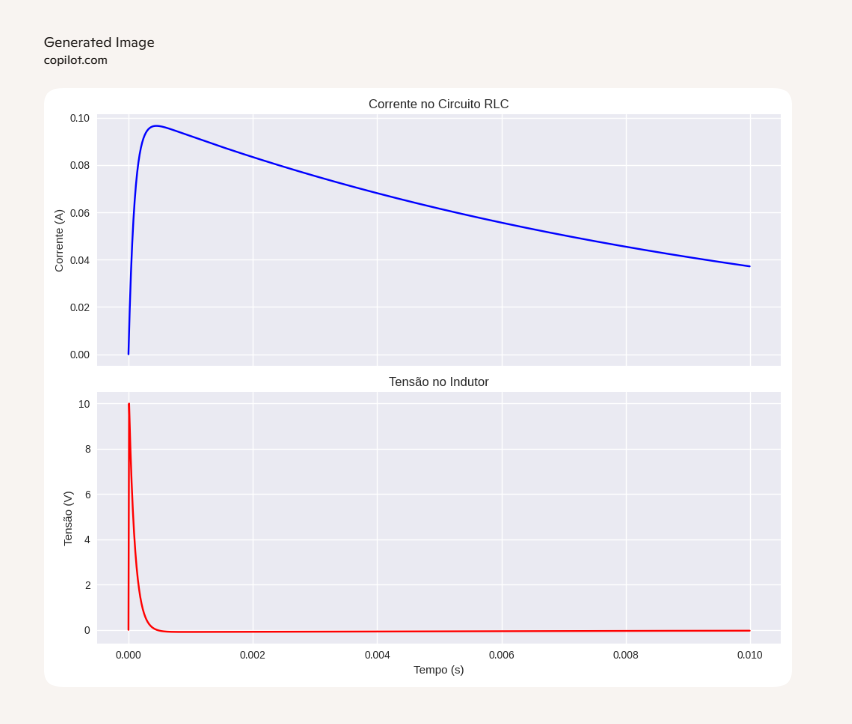
📊 Resultado esperado

• O primeiro gráfico mostra a corrente (i(t)).

• O segundo gráfico mostra a tensão no indutor (V_L), que segue a derivada da corrente.

• Se a corrente é senoidal, a tensão será também senoidal, mas defasada.

✨ Conclusão

Esse exemplo mostra como o conceito de derivada via limites se traduz em código simples, permitindo calcular numericamente a tensão em um indutor. É uma ponte direta entre matemática pura e engenharia aplicada.

👉 Quer que eu rode esse código e te mostre os gráficos prontos aqui mesmo?